Картирование структур

Давайте не забывать о том, что все так называемые знания или информация появились,
вышли из человеческой нервной системы в определённое время, в определённом месте,
и были записаны этой нервной системой при помощи каких-либо символов.
Марджери Кендиг¹ 

…У нас остаётся лишь функциональный, ориентированный на действие язык,
развитый в математическом языке функции. В таких условиях описательный язык
упорядоченных событий на уровне объекта принимает форму: «если происходит
 то-то и то-то, то происходит то-то и то-то» или кратко
«если так и так, то так и так» — это является прототипом
«логических» и математических процессов и языков.
Альфред Коржибски²

Структура. О чём вы «думаете», когда видите это слово? Возможно, вы представляете некую «вещь», например здание или его форму. Возможно, вы проводите различие между этой «вещью» и тем, что она делает, как функционирует. То есть вы отличаете «высокое здание» от «огораживает людей». 

Структура и знания

Это разделение между вещами и тем, что они делают, ведёт к традиционному отделению «структуры» от «функции» так же, как, например, анатомии от физиологии. В анатомии («подлежащем») мы изучаем структуру сердца, его клапанов, полостей, кровеносных сосудов и т.д. или на более тонких уровнях — структуру типов клеток, которые составляют эти большие элементы. В физиологии («сказуемом») мы изучаем то, что эти элементы делают — например, мы смотрим на движение крови через сердце или на электрохимические события, которые происходят при каждом ударе сердца. Мы можем сказать: «Сердце качает кровь». 

Мировые научные исследования опровергли абсолютную природу разделения. Цельные и стабильные, на первый взгляд, структуры или вещи, такие как столы, стулья, здания, сердца, мозги и т. д. можно рассматривать на субмикроскопическом уровне как события, действия или функции, как овеществление перемен.

С этой точки зрения мы можем вербально отделить ваше сердце от вашего сердцебиения, при том что оба термина относятся к процессам, действиям, которые невозможно отделить друг от друга в невербальном мире. Поэтому в общей семантике мы используем структуру слова в более широком смысле. Например, мы можем говорить о структуре вашего сердца и структуре вашего сердцебиения, структуре невербального мира и различных процессов в нём, структуре вашей нервной системы, структуре ваших опытов, восприятий и поведения, структуре языка.
Однако многие отношения можно считать асимметрическими. «Муж» и «жена» представляют асимметрические отношения. Если Сьюзан — жена Брюса, это не означает, что Брюс — жена Сьюзан. Мы не можем здесь обратить порядок так, чтобы он не потерял смысла. Схожим образом мы не можем обратить даты событий, варёное яйцо в сырое, отправиться обратно во времени, чтобы что-то изменить. Поэтому большинство отношений подразумевают асимметрический порядок: до и после, моложе и старше, больше и меньше; первый, второй, третий и т. д.

В физике и математике фигурирует поиск структуры в этом широком смысле отношений и порядка. Коржибски рассматривал в своей работе понятие «структура» как единственную сущность знаний. Для того чтобы объяснить, что он под этим подразумевал, нам нужно поговорить о картах.

Картирование

Структура карт и процесс картирования позволяют нам говорить о структуре мира и о том, как мы осмысляем его и говорим о нём. Другими словами, он дает нам возможность говорить о том, как мы приобретаем знания через процесс абстрагирования.

Стивен С. Холл писал о том, как понятие карт и картирования расширилось с начала XX века. Он упоминает статью 1910 года о карте в Энциклопедии Британнике, где было дано следующее определение: «изображение на плане в уменьшенном масштабе части или всей поверхности земли».

Холл отметил: «То узкое, связанное только с землей определение было в существенной мере концептуально дополнено после Второй мировой войны. Современное картирование простирается с атомного уровня до космического»⁴. Астрономы откартировали поверхности Луны, Марса и Юпитера. Биологи откартировали хромосомы, гены и ДНК. Нейробиологи — зоны мозга, отвечающие за зрение, осязание, память и т. д.

Действительно, понятие картирования расширилось и включает любые формы визуального представления информации. Математики Давид и Грегорий Чудновские откартировали первый миллион цифр числа Пи — бесконечно расширяющегося числа, которое получается при делении окружности круга на его диаметр. Число Пи объединяло математиков на протяжении веков, и Чудновские надеялись найти в визуальном представлении числа какие-либо повторяющиеся структуры, которые они могли пропустить, занимаясь только анализом уравнений. Их карту числа Пи, названную Pi-Scape, 1989 (Ландшафт Пи, 1989), вполне можно выставить в музее искусств⁵.

Коржибски еще больше расширил понятие картирования. Он счел данный процесс подходящей аналогией для любой формы репрезентации. Эти формы включают восприятия, картины, фильмы, видео, уравнения, слова и т. д. Коржибски рассматривал процесс абстрагирования как процесс репрезентации или картирования. 

Что мы делаем, когда создаём карту или репрезентацию какой-либо территории? Территория имеет некую структуру. Например, приблизительно с севера на юг Филадельфия находится между Нью-Йорком и Балтимором. Полезная карта или репрезентация этой территории должна быть в определенной степени схожа со структурой территории. Поэтому на нашей карте Филадельфия будет изображена между Нью-Йорком и Балтимором, а не так, что Балтимор — между Нью-Йорком и Филадельфией.

Точная карта дает нам определенную предсказуемость в отношении территории, которую она представляет. Мы хотим знать, в какое время и какого города достигнем, если будем следовать нашей карте. Если наша карта неточна, а мы с опорой на нее планируем доехать из Нью-Йорка до Балтимора к полудню, то мы разочаруемся и будем вынуждены изменить планы, когда вместо Балтимора к обеду окажемся в Филадельфии.

Когда наша карта не сходится по структуре с территориями, на которых мы хотим по ней ориентироваться, то она может завести нас не туда, куда мы хотим. Когда мы обнаруживаем это — нам стоит пересмотреть карту. Мы соглашаемся, что тщетно настаивать на том, чтобы Балтимор и Филадельфия изменили своё положение в соответствии с нашими картами и ожиданиями. Но в других сферах нашей жизни мы продолжаем пытаться подогнать территории под наши карты.



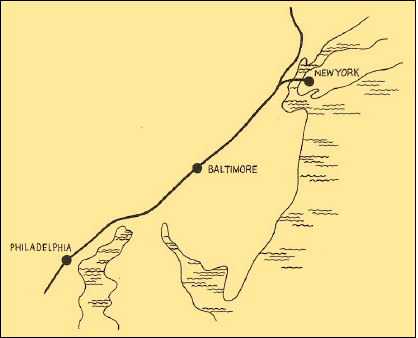
Как отметил Коржибски, независимо от того, насколько схожи по структуре карта и территория, карта это не территория. Мы называем это положение принципом не-тождественности. Репрезентация, карта, картина, описание не идентичны тому, что они представляют. Если бы карта и территория были эквивалентны, то есть идентичны, во всех отношениях, тогда какой был бы толк от карты? Представьте, что вы пытаетесь доехать из Филадельфии в Нью-Йорк, ориентируясь по карте штата Нью-Джерси, идентичной самому Нью-Джерси. Думаете, она бы уместилась в бардачке вашей машины?

Так как карта не территория, значит, она не охватывает всю территорию. Отношения, показанные на карте, могут быть схожи по структуре с отношениями, которые существуют в территории, но многие из них на карте будут неизбежно опущены. В зависимости от целей мы можем опускать одни отношения и включать другие. В этом аспекте карты нам полезны. Мы называем это принципом не-всеобъемлемости. Карты не могут включать всего, что они презентуют.

Представьте, что вы пытаетесь сделать карту, которая включает всё в вашей комнате. Это невозможно с учетом того, что мы обсудили. Тем не менее давайте рассмотрим эту задачу. Предположим, вы пытается сделать такую карту. Вы включили в нее все в комнате, о чём только могли подумать. Но включили ли вы себя за работой над картой? Хорошо, теперь вы можете пересмотреть свою карту и включить репрезентацию себя в процессе работы над картой. Осторожно! Теперь вы сделали карту себя, делающего карту. Теперь, чтобы сделать «полную» карту, вам нужно пересмотреть эту вторую карту, чтобы включить себя делающего карту себя делающего карту, тогда понадобится третья карта и т. д. Этот процесс можно продолжать бесконечно. Мы называем это принципом само-рефлексивности.

Функциональное функционирование

Мы живём в процессуальном мире различий и перемен. В структурном мире, который состоит из сложных отношений и многомерного порядка. Коржибски любил цитировать Кисера: «Быть — значит быть в отношении с чем-либо». Чтобы приобретать знания об этом мире, мы прибегаем к созданию структур, наших карт мира, схожих по структуре со структурами картируемого мира. Научное отношение, которое Коржибски причисляет к «психо-математическим методам», состоит в основном из способов использования языка и видится подходящим инструментом для картирования этого мира отношений.

Даже если упоминание о «психо-математических методах» отталкивает вас, просим все же остаться для их короткого обсуждения. Оно содержит важную вводную информацию к тому, как научиться эффективно выражать языком отношения процессуального мира различий и перемен. Без необходимости становиться физиками или математиками, мы можем научиться некоторым математическим способам использования языка, которые улучшат наше повседневное оценивание.

Сначала мы рассмотрим понятие функция, его использование в смысле, отличном от определения «то, что что-то делает». В математическом смысле «функция» означает то, как «вещи» относятся друг к другу. Пример можно найти в пятой главе, разделе о восприятии: «Степень удивления, которое мы испытываем, может быть функцией уровня осознания...» Это утверждение выражает отношение между «степенью удивления» и «уровнем осознания»: по мере того, как уровень осознания увеличивается, степень удивления уменьшается.

В предыдущем абзаце мы обособили слово «вещи» кавычками. Теперь мы можем принять математическую точку зрения в нашем рассуждении  о «вещах» и ввести термин переменные. В соответствии со сказанным мы понимаем, что нам неизвестно о количестве удивления, когда мы говорим «степень удивления», нам также неизвестна степень осознания в «уровне осознания». Среди других примеров переменных можно назвать боль в спине, тревогу, волнение и усталость. Так как каждому из этих терминов можно присвоить различные значения от низшего до высшего, в зависимости от обстоятельств мы называем их переменными.

Таким образом, переменная состоит из любой неопределенной сущности, которой может быть присвоен ряд значений. Переменные принимают определенные значения, степени и уровни, когда мы хотим конкретно описать аспекты образа действий, места и времени (как? где? когда?) в структурных отношениях и порядке.
Научные описания показывают, как переменные зависят друг от друга и изменяются по отношению друг к другу. В математике эти зависимости, или функции, символизируются как y = f(x). Это читается как «y равен f от x» (игрек равен эф от икс), или «y — это функция от x». Так, «y» и «x» обозначают переменные, а «f» обозначает функциональное отношение между ними. В этом уравнении «y» называется зависимой переменной; «x» называется независимой переменной; значение «y» зависит от значения «x».

Приведем пример: «качество наших человеческих отношений» (y) равно (=) функции (f) «понимания предположений и их последствий» (x). «Качество отношений» рассматривается как зависимое от «понимания предположений и их последствий». Это можно откартировать в форме графика, который выражает эти отношения. Посмотрите на рисунок 6-1. На нем мы картируем гипотетическое отношение между «качеством отношений» и «пониманием предположений и их последствий». Заметьте, если бы мы проводили официальное научное исследование, нам бы пришлось сделать намного больше для того, чтобы определить и описать наши переменные, провести какие-либо измерения.

Одна из наших целей заключается в том, чтобы показать, как начать говорить языком функций, переменных и т. д. Мы можем обойтись без чисел — вместо этого мы показываем участвующие отношения. Как говорил Коржибски: «Структурно, когда мы используем язык функций и переменных, мы автоматически вводим экстенсиональную (ориентированную на факты) структуру...»⁶ 



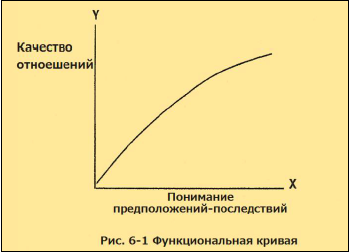
 На горизонтальную линию, называемую ось «x», мы помещаем «понимание предположений-последствий». На вертикальную линию, называемую ось «y», мы помещаем «качество отношений». Для каждого значения «x», отмеченного на горизонтальной линии, мы можем найти соответствующее значения «y» на вертикальной линии. Затем мы можем отметить точки на графике, где два значения пересекаются. Таким образом, мы показываем, что когда меняется одно значение, меняется и другое. Когда увеличивается значение «понимание предположений-последствий», увеличивается и «качество отношений».

Уэнделл Джонсон называл функциональную кривую «символом науки», когда писал следующее: «Универсальный символ науки и научного образа жизни <...> Она представляет то, что любой ученый стремится выразить: изменение одного рода, изменение другого рода и отношения между ними»⁷.

Функциональные отношения, выраженные такой кривой, помогают делать более точные прогнозы. Когда мы можем описать (присвоить значение) одному фактору, мы можем определить значения факторов, к которым он функционально относится.

Вы можете начать искать функции и переменные в ситуациях, с которыми вы имеете дело каждый день. Некоторые функции, которые мы замечаем в нашей работе с людьми, включают следующее: боль в спине может быть функцией привычек движения и поддержания осанки, типов кресел, в которых они сидят, определённого состояния их мышц и суставов, уровня тревоги и т. д. «Эмоциональное» состояние людей может быть функцией того, как они говорят сами с собой, типов их межличностных отношений, целей на будущее, историй их семей, количества потребляемого ими кофеина и т. д.

Заметьте, что определенные «следствия», как боль в спине или «эмоциональное» недомогание, скорее всего будут функциями многих переменных, которые обычно называют «причинами». Определенное «следствие» может также служить «причиной». Например, боль в спине может функционировать как причина «эмоционального» недомогания.

Бывает и наоборот, когда определённая «причина» служит переменной в нескольких различных функциях  с множеством следствий. Например, то, что вы скажете, может быть интерпретировано по-разному в зависимости от слушателей, их ожиданий и т. д. То, что вы делаете, может произвести несколько различных эффектов, которые окажутся за гранью ваших ожидаемых последствий. Когда вы имеете дело с какой-либо сложной системой или комплексом отношений, полезно вспомнить слова Гарретта Хардина, которые он сам назвал первым законом экологии: «Вы никогда не можете делать лишь что-то одно»⁸.

Не-аддитивность

Некоторые отношения происходят относительно просто и прямо. Например, представьте, что вы пригласили близкого друга на десерт, а к вашему порогу неожиданно прибыло еще четыре человека. Накрывая на стол, вы можете добавить одну тарелку и одну кружку для каждого нового человека. Таким образом, мы можем сказать, что для каждого нового человека (независимая переменная) вы добавляете два предмета из сервиза (зависимая переменная). Такое отношение называется аддитивным.

Примером аддитивных отношений может быть функция y = f(2x). Значение «y» увеличивается аддитивно, в 2 раза, по мере того, как x увеличивается на 1. Таким образом, у нас получается 2, 4, 6, 8, 10, и т. д. Каждое последующее значение «y» получается за счёт сложения предыдущего значения y с заданным количеством (в этом случае с 2). Такое отношение также называется линейным, потому что его график (кривая) выглядит как прямая линия (рис. 6-2).



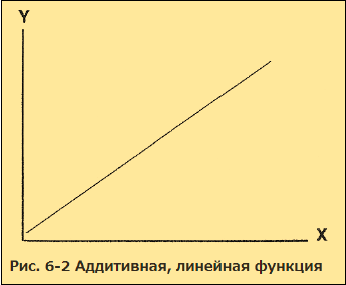
Мы можем сравнить это с не-аддитивными отношениями, примером которых может служить функция y = f(2^x). Значение y увеличивается не-аддитивно, и у нас получается 2, 4, 8, 16, 32 и т. д. Каждое последующее значение y получается путем умножения предшествующего значения y на заданное число (в этом случае на 2). Это отношение называется нелинейным, потому что его кривая, нарисованная на графике, имеет изменяющийся, а не прямой наклон (рис. 6-3).



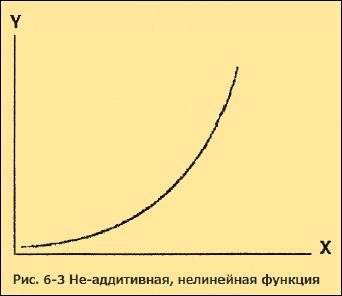
Современная математика, включая обманчиво названную теорию «хаоса»⁹, помогает нам прояснять, выражать, изображать, и таким образом лучше понимать не-аддитивные отношения. Она дает нам язык, подходящий для того, чтобы говорить о том, что мы называем многомерным порядком, сложными причинами и следствиями, отношениями и переменами в процессуальном мире, как мы его теперь понимаем.

Такие сложные факторы участвуют в большинстве наших самых важных отношений. Простой пример: образование семьи. 2 (родителя) + 1 (ребенок) = гораздо больше, нежели просто 3, потому что развивается совершенно новый комплекс отношений.

Давайте вернёмся к приглашению на десерт. Что происходит, когда ещё четверо человек прибывают? Возможно, вы хотели провести вечер за личными разговорами со своим другом. Возможно, будет не так просто изменить ваши ожидания, как добавить сервиз на стол. Для нас эта ситуация не просто 2+4=6. Что происходит, когда прибавляется каждый новый человек?

Для каждого дополнительного человека количество отношений возрастает не-аддитивно. Вы можете представить, как вы и ваш близкий друг начинаете разговаривать. Звонит дверной звонок. Вы открываете входную дверь и впускаете ещё четырёх людей. Все приветствуют друг друга, и вы приветствуете каждого. Пока вы достаете дополнительные кружки и тарелки, вы подстраиваете свои ожидания под ситуацию, обдумываете, как вы и ваши гости вместе поладите...

Экологи Пол и Энн Эрлих привели следующий пример не-аддитивности:

Ключевое свойство экспоненциального (не-аддитивного) роста состоит в том, что он начинается медленно, а заканчивается быстро. Классическим примером может послужить рдест, который каждый день покрывает площадь поверхности водоёма, равную своей изначальной площади (т. е. покрытие удваивается), и за тридцать дней вся поверхность водоема оказывается покрытой. Вопрос: какая часть площади водоема будет покрыта за двадцать девять дней? Ответ, конечно же, таков: за двадцать девять дней будет покрыта половина площади водоема. После этого рдест удвоится еще раз и покроет всю поверхность водоема на следующий день. Этот пример показывает, что экспоненциальный рост имеет потенциал для больших сюрпризов¹⁰.

Похожим образом не-аддитивно увеличивается прирост человеческого населения. Так происходит во многих других ситуациях, например со сложным процентом на вашем сберегательном счету в банке. Какие возросшие не-аддитивные следствия происходят от взаимодействия большого числа людей? Какие проблемы возникают? Что происходит со средой? Как с учетом этих сложностей могут лучше функционировать правительство, образование и т. д.?

Видимо, многие из наших политических лидеров до сих пор рассматривают данные ситуации, включающие не-аддитивные факторы, с аддитивной точки зрения. Возможно, это во многом имеет отношение к тому, что Коржибски называл «разрушаемыми» структурами. Им и нам стоит искать не-аддитивные функции в нашем нестандартном подходе, избегать нежелательных сюрпризов и развивать более устойчивые социальные структуры.

Сознательное картирование

Давайте вспомним то, о чем мы успели поговорить. Мы живём в процессуальном мире, в мире структуры, комплекса отношений с многомерным порядком. Знание подразумевает собой наличие репрезентаций или карт, которые имеют определенную структурную схожесть с какими-либо ситуациями, вещами, которые мы представляем. Мы используем аналогию с картами, чтобы говорить об этом.

У карт есть три важных характеристики, которые также служат основными принципами или допущениями общей семантики:

1. Карта — это не территория (например, слова — это не вещи, которые они представляют).
2. Карта охватывает не всю территорию (например, слова не могут охватывать всё, что они представляют).
3. Карта само-рефлексивна (например, мы говорим языком о языке)¹¹.

Для лучшего функционирования нам стоит строить наши карты с учетом оценки их структуры, отношений, порядка и функции. Поиск множества переменных в ситуациях, поиск не-аддитивных факторов помогут уменьшить количество неприятных сюрпризов в нашей жизни, потому что мы начнем ожидать неожиданного.

Человек ориентируется посредством своих моделей или карт, которые включают предположения, допущения и т. д. В той мере, в которой мы помним об этом и о других вышеупомянутых допущениях общей семантики, мы будем проверять наши карты и, как поступают ученые, пересматривать   их по необходимости.

---

¹Kendig, p. 64.