Категорный реализм

If you want more you have to assume more.
Dana Scott¹

1.

Структурализм в философии математики — это такой теоретический взгляд на математику, в соответствии с которым последняя есть исследование паттернов, или структур.

Понятые таким образом математические объекты, не имеют ни каких-то независимых, внутренных свойств, ни независимого существования, и исчерпывающим образом определяются своими отношениями с остальными объектами системы. Иначе говоря, объект существует как место в некоторой (необязательно математической) структуре². Строго говоря, структура — это единственное, что существует. Структурализм, таким образом — это разновидность математического реализма, хотя у разных структуралистов онтологический статус самой структуры может варьировать. Ante rem структурализм фактически тождественен платонизму — согласно этой точке зрения, структуры реальны абсолютно и существуют до и независимо от всяких вещей. In re структурализм ближе аристотелевской метафизике, и структуры здесь обладают существованием, только будучи воплощенными в некоторой системе объектов. И, наконец, post res структурализм, или элиминативный (чистый) структурализм отказывает в самостоятельном существовании абстракным структурам, упраздняет (элиминирует) их, сводя любые высказывания о структурах к множеству высказываний о системах — совокупностях объектов, структурированных тем или иным образом. Тогда, например, носящее откровенно метафизический характер утверждение «существует число 2» будет означать, что в любой системе, реализующей натурально-числовую структуру (т. е. такой, в которой, скажем, выполняются аксиомы Пеано), второе место не пусто. И вообще — любое высказывание Ф на языке арифметики может быть приведено к виду:

Ф′            Для любой натурально-числовой системы S верно Ф[S],

где Ф[S] получено из Ф ограничением входящих в него кванторов на совокупность объектов, образующих S, и интерпретацией всех внелогических символов в терминах существующих в S отношений.

Нетрудно заметить, что в мире, состоящем из конечного числа объектов (допустим, что их в нем не больше, чем 2⁶⁵⁵³⁶) любое предложение арифметики Ф, приведенное к виду Ф′, оказывается тривиально истинным. Действительно, ведь в таком мире не существует ни одной натурально-числовой системы, поскольку любая такая система требует существования бесконечного числа объектов. 
Таким образом, учитывая вышесказанное, представляется весьма перспективным использовать данную разновидность математического структурализма не только для обоснования математики внутри самой математики, но и как строгую онто-логическую теорию, позволяющую, как поэтично пишет в одной из своих статей Андрей Родин, формальным математическим объектам «обрести тела» (Rodin, 2010).

В качестве одной из возможных онтологий в элиминативном структурализме часто рассматриваются множества. При этом важно понимать, что теория самих множеств, во избежание бесконечного регресса, не может быть, в свою очередь, теорией какой-либо структуры. Поэтому теория множеств, берущихся в качестве основания, должна рассматриваться в обычном, не-структуралистском смысле — не как теория любых систем, удовлетворяющих набору теоретико-множественных аксиом, но как теория вполне конкретных совокупностей. Это значит, что предложения языка теории множеств уже не интерпретируются дальше указанным выше способом, а должны пониматься буквально — в частности, аксиома ZF о том, что существует множество, будет означать именно существование, со всеми вытекающими из этого утверждения онтологическими следствиями³.

Заметим следующее: говорим ли мы о стране или о некоторой части ее территории, «нашей» Галактике, или о какой-то картине художника — мы видим, прежде всего, что эти «миры» действительно состоят из элементов. Более того, если это, скажем, какая-то страна или штат, то как города данной области, так и люди, их населяющие, также принадлежат области. На языке теории множеств это означает, что элементы элементов множества также являются элементами множества. Это, вообще говоря, далеко не всегда так, но когда данное условие выполняется, то такое множество называется транзитивным⁴. Затем, множество, образованное жителями всех городов страны, т. е. ее городское население также есть элемент этой страны. То же можно сказать и об элементах звездных систем, составляющих нашу галактику — звезды, планеты, кометы, астероиды и т. п. очевидным образом лежат в той же галактике. Это значит, что сколько бы мы не дробили мир на элементы, а эти элементы, в свою очередь — снова на элементы, мы не никогда получим некой «инородной» материи, чуждой миру. Т. е., выражась формально, мир замкнут относительно операции объединения элементов его элементов. Наконец, мир не ограничен и «сверху»: если мы объединим сколь-угодно разнородные части какого-нибудь штата — новые жилые комплексы, студентов университетов, участников проводимой здесь выставки, автомобили, принадлежащие жителям — то мы получим множество, являющееся некоторым «локальным сечением» все того же штата. 
Формально речь идет о теоретико-множественных операциях, замкнутость относительно которых может быть записана следующим образом:

Множество U, удовлетворяющее перечисленным выше условиям, называется в математике универсумом Гротендика, и это то, что мы в дальнейшем и будем называть миром в сугубо онтологическом смысле. А коль скоро множества есть то, что составляет теперь нашу онтологию, и теоретико-множественные операции тоже есть, следовательно, операции онтологические, то мы можем сказать, что всякий мир онтологически замкнут. При этом можно строго показать, что размеры мира не могут быть конечными. Действительно, каким бы конечным числом мы не ограничили мощность U, применив операцию образования множества подмножеств Р(х) к любому непустому x∈U достаточное количество раз, мы превзойдем это число⁵. Следствием этого факта является то, что размеры любого мира измеряются недостижимым кардиналом. То есть, ни один мир, будучи онтологически развернут, никогда не может быть сведен к составляющим его атомам, населению и т. п.

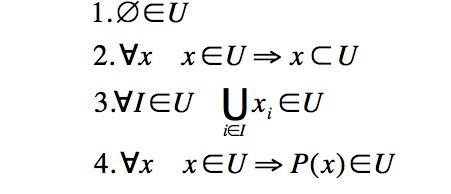
Вообще, вопрос о размерах множеств, а, соответственно, и миров заслуживает того, чтобы остановиться на нем подробнее.

Выдающийся математик Джон фон Нейман предложил в свое время две удивительно изящные и, в общем-то связванные друг с другом конструкции. Первая есть теоретико-множественное обобщение натуральных чисел, которая сейчас принято называть ординальной шкалой.

Одной из аксиом ZF является так называемая аксиома бесконечности (которая, как мы увидим, характеризует некоторый мир, но в самом мире может и не выполняться):

Правило перехода x → x∪{x}, фигурирующее в аксиоме, есть правило образования множества-последователя (successor) S(x), поскольку по данному x мы строим действительно «следующее» множество, отличающееся от данного в точности одним элементом, который есть само x. Применив правило перехода к ∅, мы получим множество-последователь S(∅)=∅∪{∅}, и это будет уже не пустота, а синглетон — множество, которому принадлежит всего один элемент: {∅}. Каким будет его последователь? Очевидно, он будет выглядеть так: {∅,{∅}}. Тогда мы можем следующим образом определить натуральные числа:

Заметим, что все три множества обладают свойством транзитивности. Но это еще не все: эти множества не только транзитивны, но и каждый их элемент транзитивен — а именно так и определяются ординалы. Любой такой ординал конечен и является ординалом-последователем. В то же время аксиома бесконечности, как мы теперь видим, утверждает, что существует предельный ординал. Среди всех предельных ординалов существует наименьший — его принято обозначать ω, и он изоморфен (канонически изоморфен) множеству натуральных чисел. Среди бесконечных ординалов тоже есть последователи, например ω+1=ω∪{ω}={0,1,2,3...ω}, но есть и предельные — например, ω+ω. Нетрудно заметить, что данную конструкцию можно продолжить и получить так называемые трансфинитные числа:

Любопытно, что все эти ординалы счетны, т. е. мощность их не превышает мощности ω, и первый ординал, мощность которого строго больше ω (и который так и принято обозначать — ω₁), есть множество всех счетных ординалов⁶.

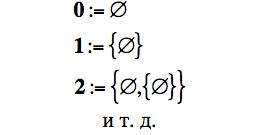
И затем фон Нейман строит свою знаменитую коммулятивную иеррархию V, где каждый «этаж» V_α ранга α — это множество всех множеств, имеющих ранг, меньший α. То есть, положив V₀:=∅, для каждого ординала-последователя β: 

а для каждого предельного ординала λ:

в результате имеем:

где α пробегает класс всех ординалов⁷.

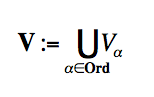
Следует обратить внимание на несколько обстоятельств:

1. Размеры «этажей» универсума фон Неймана растут необычайно стремительно. Так на V₃ находятся всего четыре элемента, на V₄ — шестнадцать, на V₅ — 65536, а на V₆ — уже 2⁶⁵⁵³⁶, что значительно превышает число атомов изученной Вселенной.

2. Объект, который, с учетом ранее принятых нами определений, можно было бы считать миром U, впервые встречается на «этаже» ранга ω, т. е. U=V_ω, где V_ω — множество всех наследственно-конечных множеств⁸, или

Таким образом, мы видим, что первый кардинал, которым измерялся бы масштаб мира, относительно небольшой — это ω, а он всего лишь счетный.

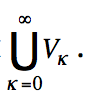
3. Несмотря на свою сравнительно небольшую мощность, ω — действительно недостижимый кардинал, так как никакие теоретико-множественные операции с конечными совокупностями не выводят нас за пределы конечного. Совсем строго свойство недостижимости можно сформулировать так: кардинал κ недостижим, если он не является суммой меньшего, чем κ числа кардиналов меньшей мощности, и ∀α < κ  2^α < κ.

4. Жителю V_ω мир представляется беспредельным (никакими имманентными онтологическими средствами предел не достигается, или, иначе говоря, понятие бесконечности не удается помыслить — вывести из остальных аксиом теории множеств) хотя мы не только знаем, что его пределом является ω, но нам также известно его (мира) точное место в коммулятивной иеррархии. Это и неудивительно, поскольку бесконечность, как мы помним, вводится в ZF специальной аксиомой, которая, разумеется, не может быть истинной в онтологии, состоящей из конечных совокупностей (несмотря на то, что число самих совокупностей может быть бесконечным). Однако, остается открытым вопрос: существует ли еще хотя бы один недостижимый кардинал, больший ω? Выше было сказано, что ω₁ это просто P(ω). Очевидно, что в онтологии, содержащей ω, достижимыми оказываются и ω₂, и  ω_n, и ω_ω, и ω_ωω....

Гротендик предлагал дополнить список аксиом теории множеств дополнительной аксиомой об универсумах: для любого множества х существует универсум U такой, что x∈U. Но можно показать, что если U — универсум Гротендика, то он обязан иметь вид V_κ, где κ — недостижимый кардинал. Верно и обратное: любой такой V_κ есть универсум Гротендика. Из чего следует эквивалентность аксиомы об универсумах аксиоме больших кардиналов: существуют сколь-угодно большие недостижимые кардиналы. Это объекты поистине невероятных размеров, свойства которых, тем не менее, могут быть системно изучены. Кроме своих захватывающих дух размеров, большие кардиналы известны еще и своими интригующими названиями. Вот лишь некоторые из них: мировые кардиналы, кардиналы Мало, Эрдоша, Рамсея, неописуемые, невыразимые, суперсильные и сильно компактные, кардиналы Вопенки и кардиналы Рейнхарда...⁹ Существование ни одного их них не может быть доказано средствами стандартной теории множеств (существование последнего даже не согласуется с аксиомой выбора, хоть пока и не опровергнуто в ZF), и должно полагаться аксиоматически, исходя из конкретных теоретических задач.

Наша же задача в этом смысле более, чем скромная: показать, что размер V_ω достаточен, чтобы в нем проявилось одно очень важное — теперь уже с логической точки зрения — и далеко не очевидное свойство: такой мир логически полон. Формальный смысл понятия логической полноты будет раскрыт ниже — и для этого нам придется снабдить нашу онтологию достаточно богатой категорной структурой. Но проделав все это, мы получим очень важный и совсем не тривиальный результат: мы строго покажем, что для любого положения дел в мире всегда найдется место, из которого данное положение дел «видимо» (здесь зрение выступает как оптическая метафора знания) единственным наилучшим образом.
Или, как сказал бы по этому поводу Витгенштейн: тайны не существует¹⁰.

2.

Здесь мы заканчиваем онтологические штудии и переходим к категорному анализу логики явления. В одной из своих последних работ «Математика трансцендентального» А. Бадью пишет: «Отвлекая данные конструкции и операции от являющеся их фундаментом множественности — и, таким образом, строго говоря, от онтологической ситуации — математики и логики смогли предложить (и это то, что составляет формальную основу самой современной логики) общую теорию возможных универсумов. В сущности, мы начинаем с букв (объектов), значение которых остается неопределенным, с отношений (стрелок), которые так же пусты, и задаем операции предельно абстрактным образом — с помощью диаграмм и алгебраических действий. Таким образом мы создаем предельно общие концепты того, что будет называться произведением или суммой двух объектов, что значит возвести один объект в степень другого, что такое расслоенное произведение двух отношений и т д. Этот минимальный набор операций на буквах и стрелках задает исходный контекст, который мы быдем называть категорией. Чем больше в категории возможно операций, тем богаче и просторнее для мысли оказыватся тот универсум, который формализует данная категория» (Badiou, 2014, 239).

Формальное определение категории чрезвычайно простое — категория С состоит из:

— класса объектов Ob C ;
— множества стрелок, или морфизмов Hom_C (X,Y) вида f : X → Y для каждой пары объектов X, Y ∈ Ob C. Объект Х называют источником, а объект У — назначением морфизма;
— для каждой пары морфизмов f и g таких, что назначение f совпадает с источником g, определена операция их композиции gof, удовлетворяющая аксиоме ассоциативности ho(gof)=(hog)of , и существует стрелка h ∈ Hom_C (X,Z) такая, что h=gof;

— для каждого объекта Х задан тождественный морфизм id_X ∈ Hom_C (X, X), причем, для любого f ∈ Hom_C (X,Y): f o id_X = id_Y o f = f. И все!

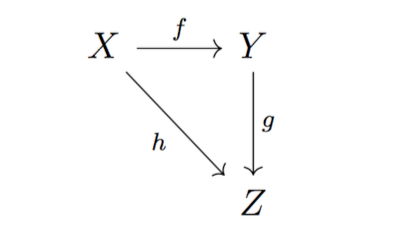
Заметим, что поскольку для любого объекта категории требуется существование тождественного морфизма, а морфизм без указания его источника и назначения недоопределен, то объекты категории сами могут пониматься как специального вида стрелки. Хотя это не всегда удобно, но, строго говоря, никто не может запретить нам думать о категории как о структурированном множестве (или классе) стрелок. Другими словами, категория являет собой некоторый единообразный тип действий, особенности которых в каждом случае выражаются в том, как именно эти действия согласовываются в последовательность (информация об этом и есть закон композиции).

С чуть более содержательной точки зрения, каждая категория — это обобщенное пространство какого-то формального дискурса. А с еще более неформальной точки зрения, в понятии категории аксиоматизируется всякое мышление вообще — ведь, если вдуматься, любую нашу мысль, любое представление о чем-то можно «изобразить» в виде каких-то объектов и определенным образом направленных от них и к ним отношений (стрелок).
Достаточно сказать, что в топосе (специального вида категории) воспроизводится (моделируется) не только вся первопорядковая логика, но и исчисления предикатов более высоких порядков.

Однако, вернемся к нашему миру V_ω. Его элементами, как мы помним, являются все конечные множества. С точки зрения онтологии, это действительно так. Но онтология имеет дело с множествами исключительно в аспекте их бытия, и ее не интересует то, как эти множества являются — какие отношения возможны между данными совокупностями в тех ситуациях, в которых мы их обнаруживаем. По-другому эту мысль можно сформулировать следующим образом: онтология как математика не занимается внутренним устройством ситуаций — ее интересуют лишь законы бытия того, что так или иначе уже есть, т. е. какого рода совокупности могут быть в принципе образованы этими существующими нечто, а также то, каковы их «теоретико- множественные» свойства. Логика же, напротив, рассматривает множества именно с точки зрения их явленности в мире. Например, с точки зрения теории множеств, нельзя быть различным «в большей или меньшей степени» — два множества либо совпадают либо нет, и это различие абсолютно. Однако, с точки зрения феноменологической, различе двух сущих зависит от того, в каком мире они были явлены¹¹.

Представляется вполне очевидным, что явление, несмотря на потенциально бесконечное число модальностей, всегда явлено в тех или иных интенсивностях этих модальностей, однако, далеко не так очевидно, что эти интенсивности являются частично упорядоченными. На этот факт в свое время указал Джозеф Гоген, ученик основателя нечеткой логики Лотфи Заде. Он пишет: «Домохозяйка сталкивается с довольно типичной проблемой оптимизации в продуктовом магазине: из всех возможных продуктовых корзин она должна выбрать ту, которая наилучшим образом удовлетворяет нескольким несовместимым критериям оптимальности — таким как цена, пищевая ценность, качество и разнообразие. Частичная упорядоченность корзин есть сущностное свойство данной проблемы» (Goguen, 1967, 145). Поэтому предложенное Гогеном обобщение теории, развитой его учителем, заключается, прежде всего, в значительном ослаблении требований к области допустимых значений, которые могут принимать случайные величины или характеристические функции множеств — непрерывный отрезок [0,1] Гоген заменяет решеткой L — частично упорядоченным множеством, в котором любые два элемента имеют наименьшую верхнюю и наибольшую нижнюю грани. Поскольку в частично упорядоченном множестве какие-то элементы могут быть несравнимы, то смысл последнего требования — в том, чтобы эти элементы все же могли быть как-то соотнесены между собой: в частности, посредством третьего «общего» элемента, который больше или, соответственно, меньше их обоих.

И вот поистине удивительным образом в математике обнаруживается объект, в точности воплощающий эту идею — таким объектом является гейтинго-значное множество. Это — сама по себе очень любопытная конструкция, позволяющая рассматриавать совокупности неких частично существующих элементов и приписывать им степени сходства (различия), принимающие значения в некотором подходящем частично-упорядоченном множестве — Гейтинговой алгебре Ω¹². Таким образом, Ω-значное множество A определяется как пара (A, Id), где А — множество, а Id — функция: A × A → Ω, ставящая в соответствие каждой паре элементов x, y ∈ A элемент p ∈ Ω, и удовлетворяющая двум условиям:

Следует отдать должное проницательности все того же Алена Бадью, который идет значительно дальше любого формального математического и даже логического контекста, и совершенно справедливо указывает на трансцендентальный характер явления. С его точки зрения, являться — значит быть («являться») значением на частично-упорядоченной шкале, которую он в своих «Логиках миров» называет трансценденталью (а функцию Id — функцией явления) (Badiou, 2009, 156).

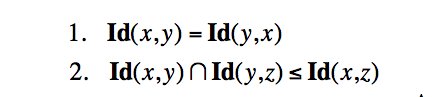
Частным случаем функции явления оказывается функция Id(x,y) при y = x, которую называют существованием элемента х и обозначают Ex. Важно, что функция Ex = Id(x,x) не обязана принимать максимально возможное значение, как того тебует обычная метрика (а две приведенные выше аксиомы функции явления делают ее в остальном действительно очень похожей на функцию расстояния) — близость, или сходство элемента с самим собой может и не быть максимальным. Это позволяет реализовать уже совсем экзистенциальную идею того, что сущее в мире может являться неаутентично, быть не равным самому себе, причем мера неаутентичности может варьировать, если так можно выразиться, от das man до dasein.

Итак, трансцендентальные значения функции явления сущностно принадлежат миру (это так даже в сугубо формальном смысле, поскольку гейтингова алгебра это, прежде всего, множество, хоть и со структурой порядка, и поэтому является элементом мира в сугубо онтологическом, или теоретико-множественном смысле), и всякое сущее всегда является в нем каким-то качеством, проявленном с какой-то интенсивностью. В различных мирах один и тот же элемент x может проявляться с различной интенсивностью p ∈ Ω, однако его явленность всегда будет иметь како-то значение, однозначно задаваемое Ω и Id. Интенсивность проявляемого качества, или свойства формально фиксируется как подобъект («подмножество») такого объекта («обобщенного множества») и определяется как функция π(x): A→Ω, удовлетворяющая некоторым двум условиям¹³, и приписывающая элементам множества А некоторые интенсивности, с которыми элементы А проявляют в мире свойство π. Значения π(x) еще можно понимать как степени, с которыми элементы множества А принадлежат «подмножеству», выделяемому в нем данным предикатом π. Таким образом, мир, мыслимый до этого лишь как чистое бытие, обретает некоторую феноменологическую (и, как мы увидим, категорную) структуру.

И еще один важный момент. Случается так, что некоторый предикат π(x) выделяет в множестве не более одного элемента, максимально проявляющего в мире свойство π, или, как мы говорили выше, выделяет в множестве А такую его часть, которой «абсолютно» принадлежит не более одного элемента. Такой подобъект (а вместе с ним, и соответствующий ему предикат π) вполне естественно назвать атомарным, или атомом. С другой стороны, мы можем рассмотреть функцию вида a(x) = Id(a,x) , ставящую в соответствие каждому элементу x ∈ A меру его сходства с некоторым фиксированным элементом а. С чисто логической точки зрения, такой функции соответствует так называемое остенсивное определение: «быть похожим на "вот это вот а" в такой- то степени». Такая функция не только атомарна (что, вообще говоря, надо доказывать), но и, так сказать, реальна — в том смысле, что мы всегда указываем на какой-то реально существующий элемент а, принадлежащий нашему миру V_ω.

Ω-значное множество A, в котором каждый атомарный подъобъект имеет вид a(x), принято называть полным Ω-значным множеством. И если мы любой атомарный предикат π смогли бы заменить на остенсивное определение вида a(x) = Id(a,x) для некоторого единственного a ∈ V_ω, то, при условии, что нам удастся корректно определить соответствующие стрелки, с V_ω можно было бы работать как с категорией полных гейтинго-значных множеств.

Cуществует канонический способ задания стрелок в категории Ω-значных множеств, но для целей настоящей работы он не так нагляден, и мы поступим немного по-другому. Заметим, что объект стал теперь устроен гораздо сложнее — теперь он сам имеет вид: A → Ω , где стрелка — это функция Id, определенная указанным выше образом. Строго говоря, эта функция не обязана оставаться одной и той же для каждого из объектов — достаточно того, чтобы она удовлетворяла аксиомам. Поэтому в дальнейшем мы будем обозначать наши объекты как пары вида (X, α), (Y, β) и т. д., указывая тем самым, что функции явления у них могут и не совпадать. Чтобы понять то, как должна быть устроена стрелка между такими объектами, попробуем сначала формализовать то, что мы будем называть отношением. Во-первых, мы хотим, чтобы это могла быть практически любая направленная связь между элементами X и Y как обыкновенными множествами. И во-вторых, отношение не должно ничего менять в онтологии — оно никак не может ни затрагивать сами элементы, ни увеличивать различия между ними. Последнее требование можно прояснить тем, что различение (например, в восприятии), достигаемое в непосредственном контакте с сущим, не может быть меньше различения, опосредованного некоторым отношением. Так мы можем определить стрелку как обыкновенную теоретико-множественную функцию f : X → Y , ограниченную следующими условиями:

Можно показать, что так определенное отношение полностью сохнаняет феноменологическую структуру объектов¹⁴, т. е. все стрелки определены корректно, и V_ω действительно образует искомую категорию¹⁵.

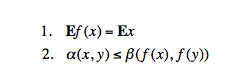
Итак, отношение, по определению, есть функциональная связь, не порождающая сущностей и различий.

Выше, цитируя Бадью, я уже упомянул, что операции в категориях задаются в том числе и с помощью диаграмм. На диаграмме действительно очень естественно и наглядно можно продемонстрировать эквивалентность «путей» от одного объекта к другому: например, на диаграмме, сопровождавшей само определение категории показано, что из Х в Z можно «попасть» либо через Y, либо непосредственно. То есть диаграмма рисуется только в том случае, если по какой-то причине уже понятно, что такое тождество путей действительно имеет место. Поэтому очень часто доказательство в теории категорий также имеет вид диаграммы: предъявленный рисунок означет, что соответствующая диаграмма коммутирует.

Изображенная ниже диаграмма может являться доказательством изоморфизма объектов X и Y, но она может означать и нечто совершенно другое:

Все зависит от того, какие «имена» мы дадим объектам и стрелкам. Если Х — это множество положительных действительных чисел, Y — множество всех действительных чисел, f — экспонета, i — умножение, а j — сложение, то мы действительно имеем перед глазами доказательство изоморфности данных структур, поскольку существует g = lnx, при которой диаграмма коммутирует, т. е. умножить что-то в Х это то же самое, что «отнести» сомножители в Y, там их сложить и вернуться с cуммой обратно в Х.

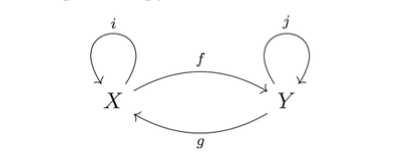
Но иногда слово «диаграмма» употребляется в категорном анализе в несколько ином смысле — как произвольный фрагмент категории, т. е. как какой-то набор объектов и стрелок.

Это часто оказывается крайне удобно для определения так называемых универсальных конструкций и категорных пределов, многие из которых также оказываются универсальными конструкциями.

Под универсальной конструкцией понимается оптимальный в некотором отношении объект категории — поэтому в указании на него всегда присутствуют слова о том, что «для любого другого «чего-то» существует единственное «что-то». Во всех таких случаях говорят, что объект обладает универсальным свойством, или что данный объект есть универсальная конструкция, поскольку в исчислении предикатов эта фраза о «любом другом чем-то» соответствует квантору всеобщности (universal quantification). Другими словами, такой объект универсален среди объектов, обладающих данным свойством. И вот оказывается, что все многообразие различных конструкций такого типа в теории категорий может быть объединено понятием категорного предела. Именно здесь и требуется «диаграмма» в специальном смысле. Итак:

— под диаграммой D в категории С будем понимать совокупность объектов d_i, d_j ... вместе со стрелками g : d_i → d_j между некоторыми объектами из диаграммы (между данной парой объектов может быть несколько стрелок, а может не быть совсем);
— конусом для диаграммы D называется такой объект с в категории С вместе со стрелками f_i :c →d_i для каждого объекта d_i из D, что диаграмма:

коммутирует для любой стрелки g из диаграммы D. Конус для диаграммы D мы будем кратко называть D-конусом.

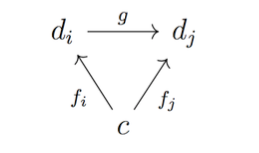
И наконец, пределом диаграммы D называется такой D-конус, что для любого другого D-конуса существует единственная стрелка f : c' → c , для которой диаграмма:

коммутирует при каждом объекте d_i из D.

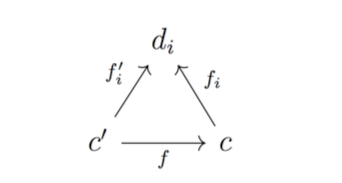
Очевидно, что, с такой точки зрения, отношение в V_ω, определенное нами выше, есть не что иное, как диаграмма вида d₁ → d₂. И тогда логическая полнота мира будет эквивалентна существованию в V_ω пределов для диаграмм D: X → Y для любых пар объектов X, Y из V_ω. Это ведь и будет означать, что любое отношение в мире может быть рассмотрено наилучшим образом, поскольку в мире всегда найдется точка, в которой данное отношение может быть продумано до своего предела. Доказательство этого положения является, вообще говоря, непростым и довольно техническим – оно выполнено полностью в монографии «Системы мысли в европейской культуре» (Egorychev, 2013, 193-200). Здесь же мы приведем лишь его набросок.

Вспомним, что мы сейчас работаем в мире V_ω как в категории, объектами которой являются гейтинго-значные множества, или пары вида вида (X, α), а стрелками – соответствующим образом определенные отношения. Таким образом, в завершенном виде доказательство представляет собой коммутирующую диаграмму, все объекты и стрелки которой конструктивно предъявлены, и доказано их существование в рассматриваемой категории.

Построение проводится в несколько этапов, на каждом из которых доказывается существование объекта определенного вида.

Утверждение 1. Для любых X,Y ∈ V_ω  X ×Y ∈ V_ω.
(Если множества принадлежат миру, то миру принадлежит и их декартово произведение, или множество всех упорядоченных пар элементов из Х и Y.)

Поскольку мир онтологически замкнут, то в нем лежит множество X∪Y, состоящее из всех элементов множеств X и Y, и множество вида X∪(P(X∪Y)), состоящее из всех элементов множества X, и всех элементов множества подмножеств множества X∪Y. Выделим теперь из данного множества элементы, обладающие следующим свойством: «быть двуэлементным множеством, первый элемент которого есть элемент множества X, а второй элемент есть пара, образованная этим же элементом множества X и каким-то элементом множества Y»¹⁶. Тем самым выделяем из множества X∪(P(X ∪Y)) все элементы вида {x,{x, y}}, т. е. все упорядоченные пары¹⁷.


Утверждение 2. Для любого отношения f между объектами (X, α) и (Y, β) в мире V_ω существует множество Z_f, элементами которого являются все упорядоченные пары вида (x, f (x)), где x ∈ X и f (x) ∈ Y.

Рассмотрим множество X×Y и выделим в нем подмножество, определив входящие в него элементы следующим образом: «быть упорядоченной парой, первый элемент которой принадлежит множеству X, а второй есть элемент множества Y, который сопоставлен данному элементу в X посредством отношения f. Выделенное таким образом подмножество Z_f (а это есть не что иное как теоретико-множественное представление графика f) является частью X×Y, или элементом P(X ×Y) ∈ V_ω, а его элементы также лежат в V_ω по свойству его транзитивности.

Утверждение 3. Рассмотрим отношение f :(X,α)→(Y, β) и множество Z_f, построенное выше. Утверждается, что в категории V_ω существует объект (Z_f, z), для которого функция явления z определена следующим образом:

Существование в мире V_ω объекта (Z_f, z) означает в точности, что данный объект удовлетворяет трем следующим условиям:
— множество Z_f ∈ V_ω (онтологическое условие);
— функция z действительно является функцией явления (логическое условие);
— все атомарные подобъекты объекта (Z_f, z) являются реальными (материалистическое условие).

Первое условие есть Утверждение 2.

Второе условие также выполняется: поскольку f — отношение, то α(x,x’) ≤ β(f (x),f (x’)). Откуда, по свойству наибольшей нижней грани¹⁸, следует, что α(x,x’)∩β(f(x), f(x’))=α(x,x’). И z можно переписать следующим образом: z[(x,y),(x’,y’)] = α(x,x’). То есть, с помощью z мы оцениваем близость двух точек на графике f, но, по построению f, нам всегда достаточно оценки близости их первых координат, а α — это функция явления по условию. Значит, остается проверить только последнее условие:

Утверждение 4. Любой атом в (Z_f , z) реален.

Чтобы это показать, выберем в объекте (Z_f,z) произвольный атом a(x,f(x)) и рассмотрим функцию a^∗ из множества X в Ω, определенную следующим образом: a^∗(x)=a(x,f(x)). Можно показать, что a^∗ есть атомарный подобъект в (X, α). Поскольку, (X, α) ∈ V_ω, то каждый атом в нем реален, и, значит, ∃!b∈X: ∀x∈X a^∗(x)=α(b,x). Таким образом, a(x, f(x)) = α(b, x) = z[(b, f(b)),(x, f(x))], т. е. z предписывается некоторым фиксированным элементом (b,f(b)) ∈ Z_f. Единственность тоже проверяется.

Утверждение 5. (Z_f, z) — конус диаграммы (X, α) ⎯⎯^f→ (Y, β) в категории V_ω. Покажем, что диаграмма, изображенная ниже, коммутирует:
  

Другими словами, нам нужно указать такие отношения g и h, что отношение f «пропускается» сквозь h (факторизуется), т.е. foh=g.

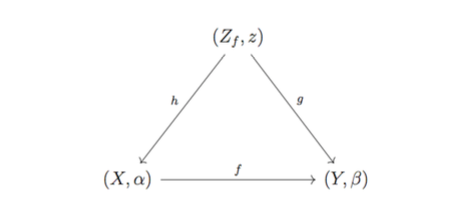
Если смотреть на g и h как на обычные функции, то кажется почти очевидным, что их надо определять как координатные проекции: т. е. каждой точке графика Z_f функция h будет определять как координатные проекции: т. е. каждой точке графика Z_f функция h будет сопоставлять его первую координату х в Х, а функция g — f(x) в Y. Понятно, что такая диаграмма не может не коммутировать. Доказательство того, что g и h — отношения, мы опустим, хотя о том, как это можно сделать, имеет смысл подумать в качестве упражнения, или внимательно разобрать доказательство, приводимое в (Egorychev, 2013, 197).

Утверждение 6. (Z , z) есть предел диаграммы (X, α) ⎯⎯^f→ (Y, β) в категории Ω-значных множеств V_ω.

Доказательство данного заключительного утверждения опять-таки представим в виде диаграммы соответствующего вида:

Нам в буквальном смысле требуется увидеть, что для для любого другого конуса (C, γ) нашей диаграммы, существует единственная стрелка k из него в (Z_f , z) такая, что треугольники CZX и СZY коммутируют. Это совсем несложно сделать. Более того, последующее рассуждение является классическим примером чисто алгебраического способа думать. Итак, поскольку (C, γ) — конус, то f o l = m, и значит, для любого элемента c ∈ C, выполняется равенство f(l(с)) = m(с). Следовательно, упорядоченная пара (l(с), m(с)) есть пара вида (x, f (x)), и, значит, (l(с), m(с)) ∈ Z_f. Тогда функцию k из С в Z_f определим следующим образом: ∀c ∈ C  k(с) = (l(с), m(с)). Мы видим, что каждому элементу с ∈ С функция k сопоставляет пару (l(с), m(с)), тогда как h сопоставляет этой паре элемент l(с) ∈ X, т. е. тот же самый, который сопоставлен с функцией l. То же верно и для второго треугольника: g — это проекция второй координаты (l(с), m(с)) в Y, т. е. g(l(с), m(с)) = m(с).

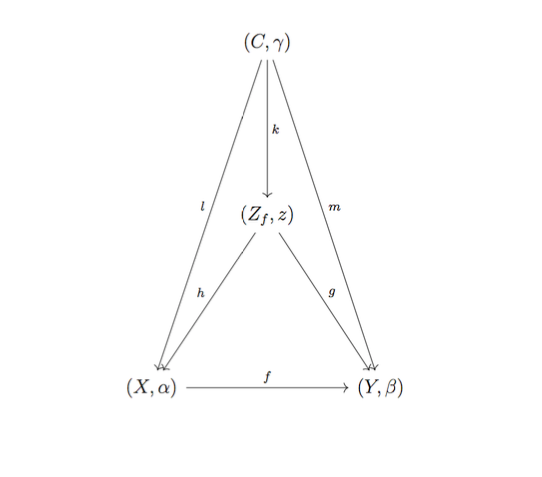
Для того, чтобы убедиться, что функция k является отношением, нужно проверить две аксиомы:

1. Ek(x)=Ex
2. α(x,y) ≤ β(k(x),k(y))

Здесь мы проверим только первую: ∀ c ∈ C  k(с) = (l(с), m(с)), а функции l и m — отношения по условию. Следовательно, k(с) = (l(с), m(с)) ⇒ Ek(с) = E(l(с), m(с)).
E(l(с),m(с)) = z[(l(с),m(с)),(l(с),m(с))] = α(l(с),l(с)) = El(с) = Ec, т.к. l — отношение.
Значит, действительно ∀ x ∈ C   Ek(x) = Ex.

Подробное доказательство того, что второе условие также выполняется, см. в (Egorychev, 2013, 199).

Чтобы убедиться в том, что отношение k единственно, достаточно понять, что именно обеспечивает коммутативность всей диаграммы, изображенной на рисунке. Очевидно, что если l(с) ∈ X, m(с) ∈ Y, а диаграмма коммутирует, то, учитывая, что функции g и h — это проекции на соответствующие координаты, это происходит только потому, что функция из С в Z_f устроена как k, которая каждому элементу с ∈ С сопоставляет пару (l(с), m(с)).
Однако, таких размеров мира (а даже Вселенная, которую мы знаем, устроена именно так) оказывается уже достаточно, чтобы, формализовав логику явления мира, мы смогли совершенно строго убедиться в так называемой логической полноте мира — содержательно проинтерпретированном свойстве категории определенного вида, в которой любая диаграмма D вида X → Y имеет предел.

---

¹ «Если хочешь большего, следует предположить большее» (цит. по: Bell, 1985, viii).

² Например, быть двойкой, значит лишь — находиться на втором месте в натурально-числовой структуре, а пешка в шахматной игре может быть с тем же успехом заменена пивной пробкой, если играющие одинаково понимают, как эту пробку можно двигать, кому и как она угрожает и т. п.

³ В своей статье "How Mathematical Concepts Get Their Bodies" Родин замечает, что сугубо формальный взгляд на аксиоматическую теорию множеств никогда не будет достаточным: поскольку для строго формального доказательства непротиворечивости ZF мы вынуждены принимать на веру формальную систему с выразительным ресурсом, превышающим ZF, то на практике остается единственный выход — работать так, как если бы аксиоматическая теория множеств была непротиворечивой, до тех пор, пока какое-то противоречие действительно не встретится. Тогда можно будет подумать, как избавить теорию от данного типа противоречий. Именно так, — отмечает А. Родин, — и создавалась современная аксиоматическая теория множеств: ее аксиомы не дают возникнуть всем известным парадоксам, но отнюдь не защищают нас от всех возможных противоречий. Схожую мысль в свое время высказывал и американский логик Хаскель Карри — говоря о приемлемости той или иной формальной системы, он формулирует три критерия: 1) интуитивная очевидность предпосылок, 2) непротиворечивость и 3) полезность. При этом Карри не требует формального доказательства непроптиворечивости системы, указывая на то, что а) этого никогда не будет достаточно, т. к. одновременно должен быть соблюден и критерий (1), и б) необходимость также сомнительна, т. к. пока выполняется (3) и не доказана противоречивость, то вообще все хорошо. А если противоречие возникло, то часто систему можно доработать. (Curry, 1954).
  
И вот чрезвычайно важная идея состоит в том, что мы не можем принять гипотезу о содержательной непротиворечивости теории иначе, чем приняв истинность аксиом — то есть должны рассматривать их как совокупность утверждений, адекватно описывающих существующий мир. (Rodin, 2010, 56-57).

⁴ В том смысле, что свойство принадлежности переносится (transit) с элемента на его элементы.

⁵ В множестве, состоящем из n элементов, можно выделить 2ⁿ частей, или подмножеств. (Поэтому множество подмножеств еще называют множеством степени.) Следовательно, применяя данную операцию к любому непустому множеству, мы получаем множества строго большей мощности и рано или поздно превысим любое заданное конечное число. Теорема Катнора утверждает, что даное свойство остается верным и для бесконечных множеств.

⁶ Ординал, мощность которого строго больше мощности ординала-предшественника, называют кардиналом. Таким образом, все конечные ординалы являются кардиналами, как и первый бесконечный ординал ω.
  
⁷ Класс всех ординалов не является множеством.

⁸ Наследственно-конечное множество (hereditarily finite set) можно определить рекурсивно как конечное множество, элементами которого являются наследственно-конечные множества.

⁹ Полный список можно посмотреть здесь: https://en.wikipedia.org/wiki/List_of_large_cardinal_properties.

¹⁰ 6.5 Для ответа, который невозможно высказать, нельзя также высказать и вопрос.
Тайны не существует.
Если вопрос вообще может быть поставлен, то на него можно и ответить (Vitgenshtein, 1994, 72).

¹¹ В мире релятивистской физики Солнце и Луна будут различаться своими массами, тогда так в мире какого-нибудь космогонического мифа они могут находиться в совершенно иных отношениях.

¹² Гейтингова алгебра — это та же решетка, но с некоторыми (важными) дополнительными свойствами. В наиболее доступной форме эта идея изложена в (Goldblatt, 2006, 274-278).

¹³ Эти условия довольно естественны и выражают две идеи: 1) что элемент не может проявлять в мире какое-то конкретное свойство в степени, большей, чем та, с которой он в этом мире существует, и 2) что то, общее, что есть у степени сходства двух элементов и интенсивности некоторого свойства, проявляемого одним из них, не может иметь интенсивность, большую, чем интенсивность проявления данного свойства вторым элементом.

¹⁴ Для этого необходимо проверить, удовлетворяют ли данным условиям обычные тождественные теоретико- множественные морфизмы, и является ли наше отношение транзитивным, т. е. если две соответствующие функции f и g удовлетворяют аксиомам, то удовлетворяет ли аксиомам их композиция.

¹⁵ В «Логиках миров» возможность замены любого атомарного предиката на остенсивное определение вида a(x) для единственного a∈Vω Бадью просто постулирует. Нам же, в одной из предыдущих работ удается показать, что возможность такой замены следует из теоремы об эквивалентности категорий соответствующего вида. См. (Egorychev, 2016).

¹⁶ Мы так можем сделать, поскольку в нашем мире выполняются все аксиомы ZFC, кроме аксиомы бесконечности, и, следовательно, мы вправе применить аксиому выделения, при условии, что предикат будет содержать параметры из V_ω.

¹⁷ В дальнейшем будем обозначать упорядоченную пару как (x, y).

¹⁸∀p,q∈Ω    p≤q⇒p∩q=p.

---

Литература

1. Badiou, A. (2009). Logics of worlds. New York: Continuum.
2. Badiou, A. (2014). Mathematics of the Transcendental. New York: Bloomsbury.
3. Bell, J.L. (1985). Boolean-Valued Models and Independence Proofs in Set Theory. New York: Oxford University Press Inc.
4. Curry H. B. (1954). Remarks on the definition and nature of mathematics. Dialectica. Vol. 8, 3, 228- 233.
5. Egorychev, I. E. (2013). Sistemy mysli v evropeiskoi kul’ture [Systems of Thought in European Culture]. Saint-Petersburg: Nauka [Science]. (In Russian).
6. Egorychev, I. (2016). Thought and Being are the Same: Categorial Rendition of the Parmenidian Thesis. Studies in Logic, Gramma and rhetoric, 46 (59), 193 — 210.
7. Goguen, J.A. (1967). L-fuzzy sets. Journal of Mathematical Analysis and Applications, 18 (1), 145- 174. doi: 10.1016/0022-247X(67)90189-8.
8. Goldblatt 2006 — Goldblatt R. Topoi. The categorial analysis of logic. — N.Y. Dover Publications Inc. 2006, P. 274-276.
9. Rodin A. 2010). How Mathematical Concepts Get Their Bodies. Topoi, 29 (1), 53-60.
10. Vitgenshtein, L. (1994). Filosofskie raboty. Chast’ 1 [Philosophical works. Part 1]. Moscow: Gnozis. (In Russian).

Оригинал публикации