Аксиома выбора

Одна из формулировок это в высшей степени загадочной аксиомы теории множеств, с точки зрения неподготовленного читателя, возможно, выглядит пугающе:

Данной аксиоме посвящены отдельные книги, по ее поводу ведутся жаркие дебаты, и вообще она представляется как предельно очевидным, так, одновременно, и совершенно мистическим утверждением¹. В ней утверждается, что мы всегда можем выбрать ровно по одному представителю из каждого непустого множества, принадлежащего данному. Говоря чуть строже, аксиома утверждает существование некоторой «функции выбора f», сопоставляющей каждому непустому множеству β, принадлежащему некоторому множеству α, один из элементов β. В случае конечных множеств никаких проблем не возникает. Но существуют такие бесконечные множества, для которых такую функцию указать не удается. В качестве чрезвычайно наглядного примера Бертран Расселл предлагал представить себе множество, состоящее из бесконечного числа коробок, в каждой из которых находится по паре ботинок. Очевидно, что мы легко можем выбрать из такой бесконечной совокупности ровно по одному ботинку из каждой коробки, всякий раз вынимая, ну, скажем, правый ботинок. Однако если ботинки заменить шнурками, то наше правило оказывается неприменимым: более того, несмотря на кажущуюся простоту операции, такого правила мы никогда не построим, и его приходится предполагать аксиоматически.

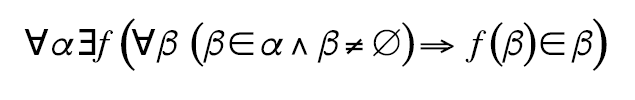
Можно возразить, что мы могли бы перенумеровать шнурки и все время выбирать шнурок номер один, но сделать этого мы также не можем: поскольку множество пар шнурков бесконечно, наша процедура нумерации никогда не закончится. Утверждение же о том, что мы в принципе способны осуществить подобную процедуру (любое множество может быть вполне упорядочено), называется теоремой Цермело и оказывается эквивалентной аксиоме выбора².

С помощью аксиомы выбора удалось сделать много математических открытий, которые были бы невозможны без нее. Однако среди следствий аксиомы есть и такие парадоксальные утверждения, которые вызывают интуитивные возражения среди части математиков. Например, появляется возможность доказать одно весьма нетривиальное утверждение, более известное как «парадокс Банаха — Тарского», суть которого сводится к тому, что шар оказывается возможным разбить на конечное число частей и сложить из них два точно таких же шара.
Онтологический запрет на событие — это, пожалуй, один из важнейших тезисов метафизической доктрины Алена Бадью, выстраиваемой им в «Бытии и событии», и который он обосновывает следующим образом.

«What is not a being is not a being»³ — цитирует Бадью Лейбница, пытаясь тем самым сказать, что еще со времен Парменида онтология всегда исходила из фундаментальной интуитивной убежденности: то, что представлено, по своей сути множественно, но то, что представлено, по сути своей едино. И тем не менее мыслить таким образом сколько-нибудь последовательно не получается. Ну действительно, если Бытие есть Единое, то множественное — это то, что не есть. Но поскольку множественное в то же время есть то, что представлено, а всякий доступ к бытию для нас возможен лишь через представление, то как мы вообще можем различить то, что себя представляет, отрицая представление? Бессилие мысли в данном вопросе очень хорошо выявлено Платоном в диалоге «Парменид», и, с точки зрения Бадью, может быть преодолено лишь так называемым аксиоматическим решением, которое необходимо имеет форму: Единого нет. Это ни в коем случае не противоречит нашей интуитивной убежденности в том, что существует единство, поскольку существует оно всегда только лишь как операция счета-за-одно, который не есть представление. Но при этом Бытие не есть также и Многое, так как Многое нам дано только в представлении...

Итак, Многое есть режим представления; Единое в отношении к представлению есть результат операции; Бытие есть то, что представляет себя. Исходя из сказанного, Бытие не есть ни Единое (поскольку только о представлении осмысленно говорить, что оно было сосчитано-за-одно), ни Многое, поскольку Многое есть всего лишь режим представления⁴.

Всякое представленное множество Бадью предлагает называть ситуацией, или тем местом, где нечто имеет место⁵. Каждой ситуации присущ свой оператор счета-за-одно, и задать такой оператор — значит, задать структуру ситуации в самом общем смысле: структура есть то, что предписывает представленному множеству некоторый режим счета-за-одно. Таким образом, всякая ситуация структурирована, и ее множественность лишь ретроактивно мыслится предшествующей Единому и лишь постольку, поскольку счет-за-одно всегда уже есть результат. Тот факт, что Единое есть операция, позволяет нам (также всегда находящимся в какой-то ситуации) предполагать, что то, в отношении чего она применяется (ее домен⁶), не есть Единое, и, следовательно то, что, не есть Единое, является множеством внутри представления, то есть, это множественность, проявляющаяся как некая инерция ситуации, в которую сама оппозиция единое/многое инсталлируется счетом-за-одно. Онтологический статус представленного, таким образом, оказывается фундирован как множественнсть, «за кулисами» процедуры счета. И такую множественность, которую Бадью называет неконсистентной, следует отличать от любых последующих объединений в множества уже сосчитанного-за-одно, которые всегда есть множественность консистентная, или структурный эффект.

Итак, все, что представлено, есть множество, и, следовательно, нет ничего, кроме ситуаций, и онтология, если она вообще существует, также является одной из ситуаций. Означает ли это, что представленность Бытия является необходимой? Бадью полагает, что нет — скорее, Бытие входит в то, что представлено любым представлением, но само как таковое, никогда не представлено. Разумеется, множественность представления в структурированной ситуации — а они все такие — это такое множество, которое было собрано на базе действующего в ситуации оператора счета. И все же представление вообще, благодаря ретроактивному действию оператора счета-за-одно, позволяет как бы «по инерции» полагать тот нередуцируемый к представленной множественности домен, на котором был определен данный оператор. И этот домен и есть Бытие — чистая неконсистентная множественность.

Мы видим, таким образом, что всякая ситуация действительно фундирована ничто, или пустым множеством ∅⁷ — именем неконсистентной множественности, которая есть бытие. И в то же самое время ни одна ситуация, не являющаяся онтологической, не может допустить осознания этого факта. Это полностью обрушило бы ее структуру, прямо указав на ничтожность любого принципа счета-за-одно. В этом смысле забвение бытия характерно не только для математиков, занимающихся онтологией, не ведая, что они творят именно онтологию, но и является конституирующим принципом стабильности ситуации вообще. Столкновение с ничто, таким образом, невозможно, но угроза Реального, как назвал бы это Лакан, остается более чем реальной, и это происходит потому, что в ситуации, любые устойчивые единства которой есть результат счета, сам счет оказывается не посчитан. Он не принадлежит ситуации и поэтому не существует для нее. Поэтому нужен какой-то другой счет, который бы навсегда узаконил первый и не оставил бы никакой возможности для представления ничто в ситуации. Эту функцию «забвения» и берет на себя множество степени⁸ Р(α) (Бадью называет его метаструктурой, или Режимом⁹), существование которого формально гарантировано соответствующей аксиомой и необходимо по следующим причинам: существует теорема, утверждающая, что мощность множества подмножеств любого множества строго больше мощности самого множества (теорема Кантора). Это означает, что частей во множестве всегда больше, чем его элементов, т. е. в любой ситуации необходимо существуют подмножества, которые, будучи частями ситуации, однако, не принадлежат ей, а значит, не существуют для ситуации. Эти части и являются потенциальными носителями ничто (пустое множество является подмножеством любого множества), способными поставить под сомнение основания любого порядка, — поэтому необходимо должен быть введен режим, который бы препятствовал образованию подобных «зон хаоса» (в случае ситуации политической слово state, которое использует Бадью, звучит наиболее узнаваемо, поскольку в данном случае функцию метаструктуры выполняет, конечно же, государство).
И все же она — метаструктура ситуации, поскольку репрезентирует лишь то, что представлено в ситуации. Таким образом, мы можем выделить три типа элементов в зависимости от их «затронутости» операторами презентации и репрезентации, соответственно:

1. нормальный элемент — принадлежит ситуации и одновременно является ее частью. Следовательно, представлен как структурой (ситуацией), так и метаструктурой (репрезентирован);
2. избыточный элемент — не принадлежит ситуации (не представлен), но является ее частью и, следовательно, репрезентирован метаструктурой;
3. сингулярный элемент — принадлежит ситуации, но не является ее частью.

Существование таких элементов Бадью называет бытием-на-грани-ничто: несмотря на то что они очевидным образом присутствуют в ситуации, их существование тем не менее не верифицируется никаким режимом. Такие элементы всегда «вне закона», и их присутствие может быть распознано только благодаря их вовлеченности в какие-то иные части ситуации, представленные (репрезентированные) метаструктурой.

Здесь необходимо сделать два замечания. Во-первых, из сказанного следует, что у онтологии (как ситуации) нет своей метаструктуры, и поэтому лишь она одна допускает мысль о ничто. Более того, именем собственным ∅ она «подшивает» свой дискурс к бытию как неконсистентной множественности. Это также значит (и это во-вторых), что никакая не-онтологическая ситуация не может быть фундирована ничто: хоть аксиома регулярности (о ней чуть ниже) и гарантирует наличие сингулярного элемента в любой ситуации, из этого вовсе не следует, что этот элемент — ∅. Наоборот, в любой не- онтологической ситуации существует, по крайней мере, один сингулярный элемент δ, который не пуст.

Дальше. Сингулярное множество, ни один элемент которого не представлен в ситуации, Бадью также называет событийным сайтом и исторической (в противоположность природной) — ситуацию (а всякая ситуация, как мы помним, является множеством), которой принадлежит хотя бы один событийный сайт. Важно, что данное определение локально: одно и то же множество может быть сингулярным в одной ситуации, но нормальным — в другой, в то время как природная ситуация (нормальное множество, каждый элемент которого нормален¹⁰) сохраняет свои свойства в любых обстоятельствах. Что дает нам право заключить: природа абсолютна, историчность относительна. Сингулярности всегда могут быть нормализованы, но невозможно заставить природу быть историчной. Таким образом, бессмысленно говорить о событии-в-себе, поскольку последнее есть всегда событие для кого-то и в отношении той конкретной ситуации, в которой оно было представлено. Разумеется, наличие событийного сайта в ситуации не влечет за собой необходимости наступления события, однако оно является его необходимым условием.

Итак, дадим определение события: пусть Х — событийный сайт. Тогда событием сайта Х назовем множество:

То есть это множество, состоящее из всех элементов сайта Х и самого события.

Чтобы показать, что данное определение соответствует нашему интуитивному пониманию события, давайте вспомним всем нам хорошо известное событие Октябрьской революции: оно представлено в нашей памяти (в истории) как множество людей, совершавших какие-то поступки, как множество каких-то других мелких событий, произошедших в определенный исторический период, и т. п. Но также очевидно, что все эти мелкие события и поступки совершались «именем революции» и «во имя революции», что все эти люди были всецело преданы тому, чего еще нет, что еще только может случиться (или не случиться), и поэтому означающее события должно быть в нем также представлено. Другими словами, «имя революции» есть необходимый элемент события Октябрьской революции, и значит, наше определение корректно.
Возможность первая: событие не принадлежит ситуации. В таком случае оно никак не может быть различено. Помимо своего имени, в событии как множестве представлены только элементы событийного сайта, но они не представлены в ситуации. Если же, по предположению, и оно само не представлено, то с точки зрения ситуации оно ничего собой не представляет, кроме «пустого означающего», которое хоть и было «контрабандой» втянуто в ситуацию «революционными» действиями элементов событийного сайта, но референтом их действий всегда будет пустота (всегда можно сказать, что «они сами не знают, о чем болтают»...).

Возможность вторая: событие принадлежит ситуации. Тогда оно должно быть сингулярным. Если бы оно было нормальным, то все его элементы были бы также частью ситуации, но это невозможно, так как его элементы — это и элементы сайта, а они, по условию, не представлены. Поэтому событие немыслимо в терминах метаструктуры (что согласуется и с интуицией — например, рабочие завода не мыслятся государством как революционеры). Но тотальной сингулярности события препятствует принадлежащее ему означающее себя самого, которое обретает свой смысл, становится Событием, как только мы признаем, что событие принадлежит ситуации: e_x ∈ e_x.

Такие множества, являющиеся элементами самих себя, математики иногда называют «парадоксальными», и таким образом мы могли бы заключить, что Событие формализуется в теории множеств как такое «парадоксальное множество». Однако прямым следствием аксиомы регулярности¹¹ является запрет на любые «парадоксальные» множества, являющиеся элементами самих себя. Действительно, рассмотрим множество α такое, что α ∈ α. Если оно существует, то существует и его синглетон{α}¹². Но существование такого синглетона противоречило бы аксиоме регулярности, поскольку α∩{α} = α (т. к. α ∈ α и α ∈ {α}).
А что же аксиома выбора? Давайте еще раз обратим внимание на то, что она утверждает. Функция выбора, по сути, гарантирует существование множества γ, составленного из представителей каждого непустого элемента множества α (напомню, что в аксиоматической теории множеств Цермело- Френкеля есть только один тип объектов — множество. Поэтому любой элемент множества сам может быть только множеством, т. е. тоже содержит элементы): 

Но гарантия эта существенно отличается от других аксиом. Если мы внимательно рассмотрим любую из них, то увидим их «конструктивный» характер: все свойства конструируируемых с их помощью множеств всегда явно определены. В случае же аксиомы выбора это далеко не так — говорится весьма уклончиво:

(см. формулировку, приведенную в начале статьи). Но ни о том, как эта функция зависит от внутренней структуры множества α, ни о том, единственна ли такая функция, ничего не сообщается. Аксиома выбора, по большому счету, ставит в соответствие некоторому существующему множеству возможность множества его представителей, существование которого никак невозможно удостоверить, поскольку не указано никакого алгоритма реализации такой возможности, который можно было бы применить, сообразуясь с конкретным устройством исходного множества.

Итак, мы не располагаем ни законной процедурой, следуя которой мы могли бы выбирать представителей, ни, более того, возможностью хоть как- то отличать друг от друга тех, кого выбрали. Согласитесь: сходство с «примкнувшими к делу революции» поистине ощеломляющее! И оно неслучайно, поскольку речь в аксиоме выбора несомненно идет о событии. Точнее, это то немногое, что о нем способна высказать онтология. Таким образом, нелегальность и анонимность функции выбора — это цена, которую приходится платить Субъекту за такое бытие, в котором возможно новое. Другими словами, вопрос о том, имело или не имело место в ситуации событие, всегда должен решать сам Субъект — онтология лишь в принципе не исключает такую возможность, однако не раполагает для реализации этой возможности никакими инструментами.

____

¹ Бертран Рассел так отозвался об аксиоме выбора: «Сначала она кажется очевидной, но чем больше вдумываешься, тем более странными кажутся выводы из этой аксиомы; под конец же вообще перестаешь понимать, что же она означает».

² В русскоязычной Википедии, в статье с названием «Лемма Цорна» есть такие строчки: «В 1904 году Эрнст Цермело доказал теорему, согласно которой каждое множество может быть вполне упорядочено. Для доказательства он привлек "неоспоримый логический принцип", который назвал аксиомой выбора. Сегодня мы знаем, что аксиома выбора, теорема Цермело и лемма Цорна — эквивалентные утверждения». (См. https://ru.wikipedia.org/wiki/Лемма_Цорна) Всего три строчки, но я убежден, что всякий, кто честно постарается понять то, что именно в них утверждается, и что означает эта эквивалентность, сам, в свою очередь, может смело утверждать, что в теории множеств он разбирается очень и очень неплохо. 

³ Что не есть бытие отдельное, то не есть бытие вообще. 

⁴ Badiou A. Being and Event. Continuum, N.Y. 2007, Р. 24 

⁵ place of taking-place.

⁶ Описывая те или иные функции, принято различать их области определения и области значения. В английском языке этим понятиям соответствуют слова domain и range, которые представляются гораздо более удачными. Неслучайно философы чаще пользуются именно последними, говоря, к примеру, о «доменах действительности». 

⁷ С формальной точки зрения, пустое множество действительно является частью (подмоножетвом) любого множества. 

⁸ Множество подмножеств некоторого множества А часто называют множеством степени, поскольку оно состоит из € 2A элементов (возведение в степень А здесь понимается с точки зрения числа принадлежащих А элементов). 

⁹ В оригинале — state of the situation.

¹⁰ Определение природного сайта есть в точности определение ординала — транзитивного множества, каждый элемент которого транзитивен

<sup>11 

12</sup> В теории множеств Цермело-Френкеля существование пустого множества ∅ полагается аксиоматически. Применяя к нему аксиому существования множества частей (подмножеств), получаем синглетон {∅} и по аксиоме подстановки заменяем в нем ∅ на α.